Draw Julia set animations by simply defining a 2d line though the complex plane.
A Julia set is simply a recursive function or iterative process that takes the form z=z^2+c
where the initial value of z is a complex number representing a point in 2d space, and c is any complex.
The z argument is updated until the desired number of iterations, or until it’s magnitude exceeds 2, if it exceeds 2 then we know it will eventually trend to infinity and it’s in the set.
A general definition may look something like this:
def julia(z,c,iterations=10):#z and c are both complex numbers (they may be solely imaginary or real but usually a mixture of the two)
if abs(z)>2: #if the magnitude of z is greater than 2, the point is outside the julia set
return False
elif iterations<=0: #If the desired amount of iterations have elapsed and z still doesn't have a magnitude of at least 2 then that point can be considered in the set.
return True
else: #If iterations still remain and the magnitude of z is under 2, the recursively call the julia set function again, with z replaced by z squared + c and iterations replaced with iterations-1.
return julia(z**2+c,c,iterations-1)This function is then mapped to a (usually 2d Euclidean) space, represented as complex numbers (x+yi), ,and it’s features can be zoomed/scaled to reveal more details indefinitely.
This mapping in its simplest form may look like this:
def complexgraph(func,minX=-1,minY=-1,maxX=1,maxY=1):
resolution=(1080,720)
xdifference=maxX-minX
ydifference=maxY-minY
out=[]
for i in range(resolution[0]):
row=[]
for j in range(resolution[1]):
x=minX+xdifference/resolution[0]*i
y=minY+ydifference/resolution[1]*i
z=x+y*1j #in python the imaginary number is j (it's an electricians convention where I already means current)
row.append(func(z))
out.append(row)
return out
#With the Julia set called as such
complexgraph(lambda z:julia(z,.62-.75j))
#This will make the julia set c=.62-.75j
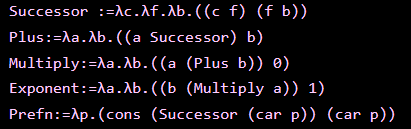
My current definition for animated Julia sets is as follows
from __future__ import division
from PIL import Image,ImageDraw
def julia(b,c,d,iterations=30):
c=c+d*1j
def inner(x,y):
z=x+y*1j
for i in range(iterations):
z=z**b+c
absol=abs(z)
if absol<2:
return (60+(absol%2)*50,64+(absol%2)*40,(64+(absol**1.1)%2)*90)
return (absol*260,absol*80,absol*140)
return inner
def drawfunc(f,resolution=(1080,720),view=(-1.2,-.7,1.2,.7),frame=0):
resolution=(int(resolution[0]),int(resolution[1]))
im=Image.new("RGB",resolution,(0,0,0))
for i in range(resolution[0]):
for j in range(resolution[1]):
x=view[0]+(view[2]-view[0])*i/resolution[0]
y=view[1]+(view[3]-view[1])*j/resolution[1]
col=f(x,y)
col=tuple([int(min(255,max(0,i))) for i in col])
im.putpixel((i,j),col)
im.save("A%04d.png"%frame)
def midpoint(a,b,r):
return a+(b-a)*r
def drawpath(b1,b2,c1,c2,d1,d2,resolution=(1080,720),iterations=6,steps=10000):
for frame in range(2000,3000):
r=frame/steps
drawfunc(julia(midpoint(b1,b2,r),midpoint(c1,c2,r),midpoint(d1,d2,r)),resolution=resolution,frame=frame)
drawpath(2,2,-.8,-1.2,.4,-.2)While quite short it can produce an endless array of intricate patterns and pairing with a kaleidoscope can force symmetry and produce amazing shapes.
Here are a few renders I’ve made throughout the years:
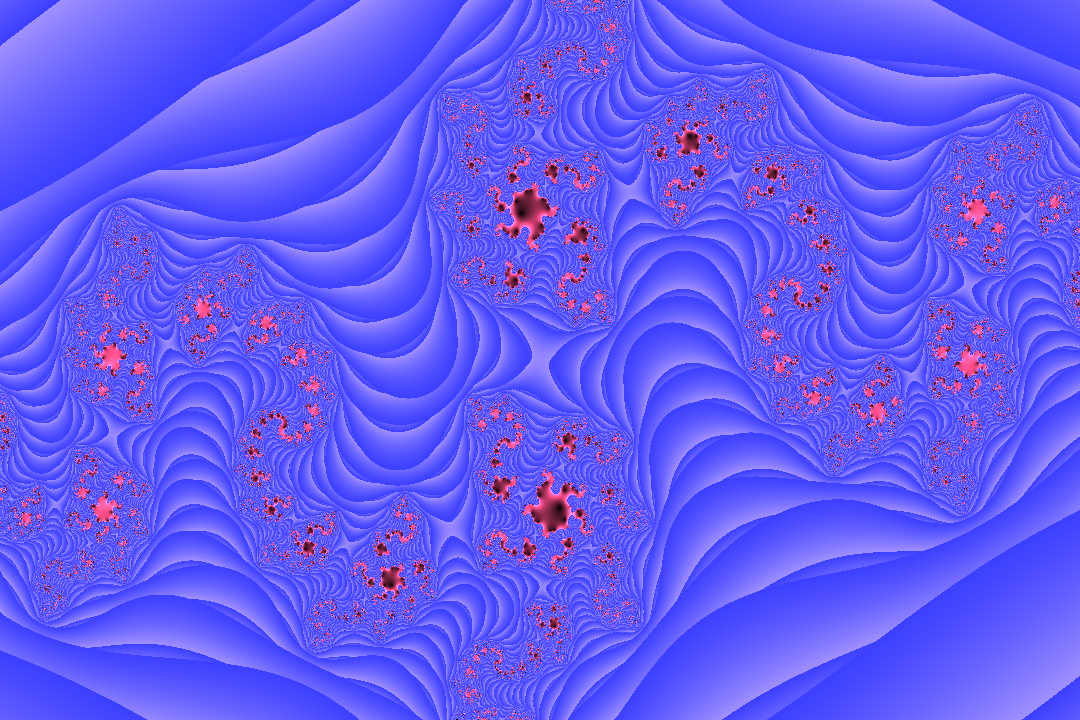







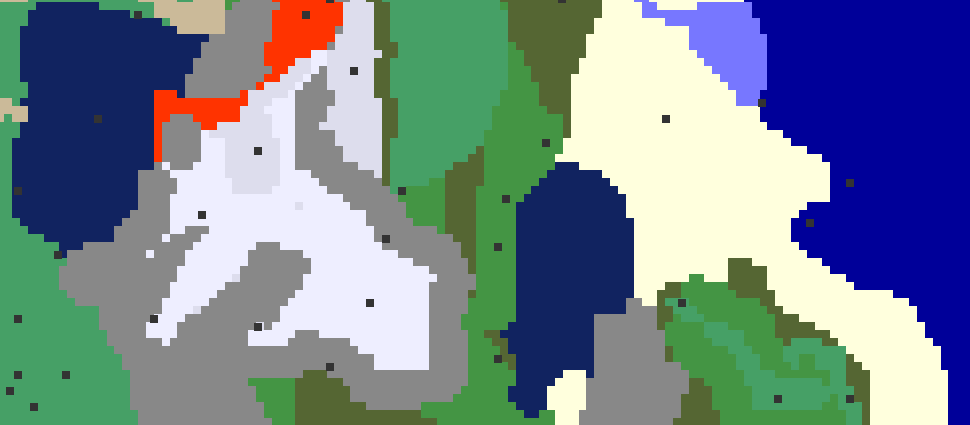






0