Introduction
Here I’ve written and uploaded a great deal of untyped Lambda Calculus functions, and will continue to expand upon them quite regularly. I’d like to try and get deep enough into the arithmetic of integers to be to be able to perform some introductory geometry, but I hope to take it much much further.
If you’re unfamiliar with lambda calculus don’t start here, maybe check out the Wikipedia, for the time being, and I’ll aim to compile some better resources shortly.
Please read before continuing!
Notation (quoted directly from Wikipedia)
To keep the notation of lambda expressions uncluttered, the following conventions are usually applied:
- Outermost parentheses are dropped: M N instead of (M N).
- Applications are assumed to be left associative: M N P may be written instead of ((M N) P).[17]
- The body of an abstraction extends as far right as possible: λx.M N means λx.(M N) and not (λx.M) N.
- A sequence of abstractions is contracted: λx.λy.λz.N is abbreviated as λxyz.N
I will not be using any of these shorthand syntax rules! I’m doing the full masochist drowning in parentheses version; if we wanted convenience we wouldn’t be using untyped Lambda Calculus. Writing the unabridged syntax will make it a little more convenient to programmatically convert the declarations into other functional programming languages.
I’ve curried every function, each variable must be proceeded by it’s own lambda, if you see a lambda followed by more than one characters before its accompanying period it means I’ve given the variable a multiple-character name, which I would only do if I feel it will be ambiguous without it.
In future I intend to make a javascript lambda calculus interpreter so I can embed some step by step beta-reduction demos on the site.
Check back regularly as this page will be updated a lot; my plan is to get deeper into lambda calculus than than anyone before.
Boolean Logic
True:=λa.λb.a
False:=λa.λb.b
And:=λa.λb.((a b) False)
Or:=λa.λb.((a True) b)
Not:=λa.((a False) True)
Xor:=λa.λb.((a (not b)) b)
Data Structures (Pairs, Lists, Trees)
cons:=λa.λb.λz.((z a) b)
;;Given arguments a & b it results in an ordered pair awaiting argument z at which point it will apply a to z apply b to the result. This structure can be beaded into others and is the basic building block of LISP family languages.
car:=λc.(c True)
;;;Access the first item in an ordered pair, vector, list, tree, or any other structure encoded with beaded cons cells
cdr:=λc.(c False)
;;;Access the second item in an ordered pair, or every item in a list but the first.
nil:=λc.True
;;Used to signify the end of a beaded cons structure, usually a list.
null:=λc.(c λa.λb.False)
;;Returns true if a List Functions
map:=λf.λl.(((null l) nil) ((cons (f (car l))) ((map f) (cdr l))))
;;map recurses through every item in a beaded list of cons cells, until it finds a terminating nil, and returns a list of equal length where the left hand side of every cons-cell has been applied to the function 'f.
foldr:=λf.λl.λa.(((null l) a) (((fold f) (cdr l)) ((f a) (car l))))
;;recurse through a list of (right) beaded cons cells applying a combining operation to each item and the accumulating value.
Sum:=λl.((foldr plus l) 0)
;;A nice demonstration of
filter:=λf.λl.(((null l) nil) (λr.(((f (car l)) ((cons (car l)) r)) r) ((filter f) (cdr l))))
;;Filter a list, keeping elements (car l) only when (f (car l)) is True
Arithmetic
Whole Numbers
0:=λf.λb.b
1:=λf.λb.(f b)
2:=λf.λb.(f (f b))
3:=λf.λb.(f (f (f b)))
...
10:=λf.λb.(f (f (f (f (f (f (f (f (f (f b))))))))))
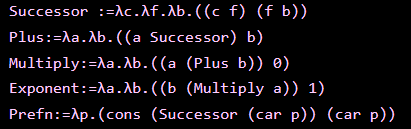
Successor :=λc.λf.λb.((c f) (f b))
Plus:=λa.λb.((a Successor) b)
Multiply:=λa.λb.((a (Plus b)) 0)
Exponent:=λa.λb.((b (Multiply a)) 1)
Prefn:=λp.(cons (Successor (car p)) (car p))
;;In non-lambdaspeak prefn just takes an ordered pair (A,B) and returns (A+1,A) it's a vital part of the predecessor function.
Predecessor:=λc.(cdr ((c Prefn) ((cons 0) 0)))
;;Apply Prefn C times to ((cons 0) 0) returning the value ((cons C) )))
;;Returns the value below below the input number;;
Subtract:=λa.λb.((b predecessor) a)
Integers
;;There are quite a few ways integers could be done, keeping with the theme of church numerals you could either add an extra argument for an inverse; nesting the base within recurring functions for positive, or recurring inverse functions for negative.
int0:=λf.λg.λb.b
int+1:=λf.λg.λb.(f b)
int+2:=λf.λg.λb.(f (f b))
int+3:=λf.λg.λb.(f (f (f b)))
int-1:=λf.λg.λb.(g b)
int-2:=λf.λg.λb.(g (g b))
int-3:=λf.λg.λb.(g (g (g b)))
;;This method has the obvious advantage of a super simple pred function, which is just an isomer of successor
Succ:=λc.λf.λg.λb.(((c f) g) (f b))
Pred:=λc.λf.λg.λb.(((c f) g) (g b))
;Of course this has many obvious disadvantages. The simplicity might make it preferable in a few domains, aside from acruing huge strings redundencies, the most glaring hole is that not all functions have an inverse.
;;I won't go any further building on these definitions, but if anyone else does please contact me as I'd love to see where it takes you.
;Instead I'll be implementing the integers as signed church numerals (I'll redeclare some better numbers just down the page, but they're still dependent on these definitions)
Int:=λp.λc.((cons p) c)
;;p is true if the integer is positive, false if its negative & c is a church encoded whole number representing the magnitude
int-succ-cdr:=λi.((cons (car p)) (successor (cdr p)))
int-pred-cdr:=λi.((cons (car p)) (predeccessor (cdr p)))
int-succ:=λi.(((car i) (int-succ-cdr i)) (((zero? (cdr i)) ((cons True) 1)) (int-pred-cdr i)))
int-pred:=λi.(((car i) (((zero? (cdr i)) ((cons False) 1)) (int-pred-cdr i))) (int-succ-cdr i))
int-plus:=λa.λb.(((car b) (((cdr b) int-succ) a)) (((cdr b) int-pred) a))
int-subtract:=λa.λb.(((car b) (((cdr b) int-pred) a)) (((cdr b) int-succ) a))
BASE N ENCODING OF INTEGERS
;;From here own I'm going off the beaten path, things might get weird.
;;Temporarily switching to a syntax where (A.B) means (cons a b)
;;a base 10 number would look like this (10 .((((nil . 3) . 2) . 1) . 0))
;;or in our full syntax ((cons 10) ((cons ((cons ((cons ((cons nil) 3)) 2)) 1)) 0))
;;This represents 3210 in base 10
baseN_plus_inner=λB.λL.λM.λC:
((null? L)
((null? M)
((zero? C) nil (cons nil C))
(cons (baseN_plus_inner B nil (cdr M) (div (plus (car L) C) B)) (mod (plus (car M) C) B)))
((null? M)
(cons (baseN_plus_inner B (cdr L) nil (div (plus (car L) C) B)) (mod (plus (car L) C) B))
((cons (baseN_plus_inner B (cdr L) (cdr M) (div (plus (plus (car L) (car M)) C) B)) (mod (plus (plus (car L) (car M)) C) B)))))
baseN_plus=λa.λb.(cons (car a) (baseN_plus_inner (car a) (cdr a) (cdr b) 0))

0