In future I will expand this into a database, however for the time being this page will suffice.
I created this page to index the positions of the interesting fractals that appear using recursive operations on complex numbers.
The most famous complex-number fractals are certainly the Julia Sets and the Mandelbrot Set.
I’ll be sure to cover the Mandelbrot and Julia sets, but since many others are doing exactly this I will try to focus on less known equations.
This page will get pretty massive, so I might put in some collapsible divs once I add a couple more functions.
The plan is to switch it to a database fairly soon so I don’t want to develop this page too much.
z=1/(1-z^2)+c








z=c/(1-z^3)-c





z=z^z-c/(1-z^2)
Contains beautiful chaotic patterns, predominantly on the left hand-side, for some c values these stretch a very long distance, but become larger the further left you go.




As the imaginary value trends higher the details become confined closer to (0,0)


For imaginary values that aren’t too far from 0, as the real component of c drops below -1 the shapes become closed and their boundaries a lot more clear.

Keeping the imaginary value fixed on -.3i, the internal fractals disappear around -1.25-0.3i.
This may be a point of interest for those who like to zoom-in and explore the deeper details.


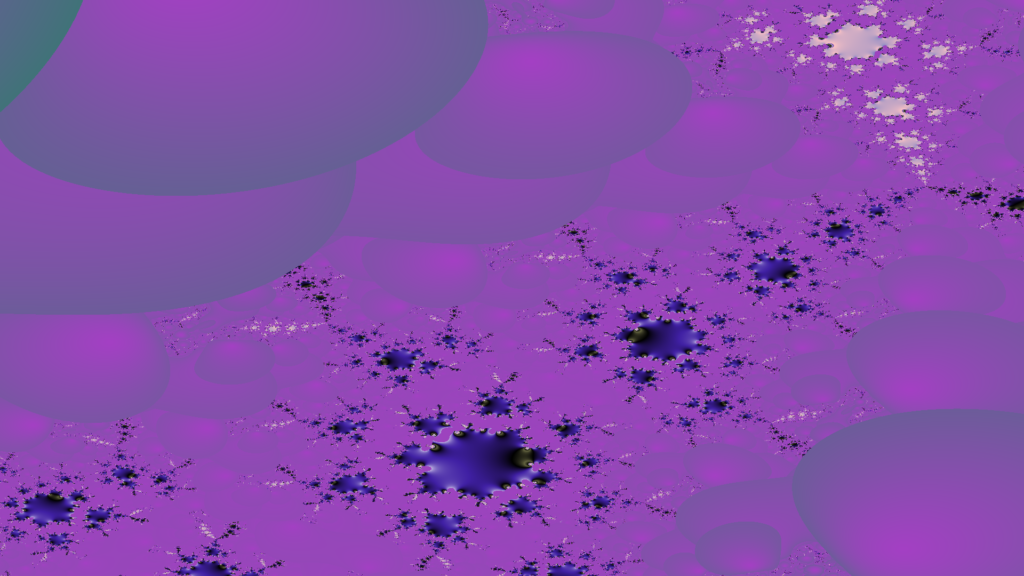

The ideal range seems like
-1.1 to -0.8 or 0.8 to 1.1 for the real values, and,
-1.2 to -.2 imaginary value when the real value is negative, or,
positive or negative .18 to .6 as an imaginary value when the real value is positive.
z=z^2+c (Julia-Sets & Mandelbrot Set)
Recursions of Two Complex Numbers
Usually each Julia-Set, or any related fractals made with recursions on the complex-plane, only use a single, usually complex, “Magic Number” commonly identified as c.
The following functions use two magic numbers which I will label c and d respectively.
z=z**4/(z+c)/(z+d)+(c+d)/2

d=0.8541587+1.67580i

d=0.43161579+0.6802431i

d=1.75854753+1.466066i

d=0.69686-0.558667i

d=0.00183825+0.2405473i

d=1.323942-1.02991i
c/(1-z^2)+d

d=-0.74911173+1.137821i

d=-0.8388+0.39069i

d=-0.445322-1.896184i
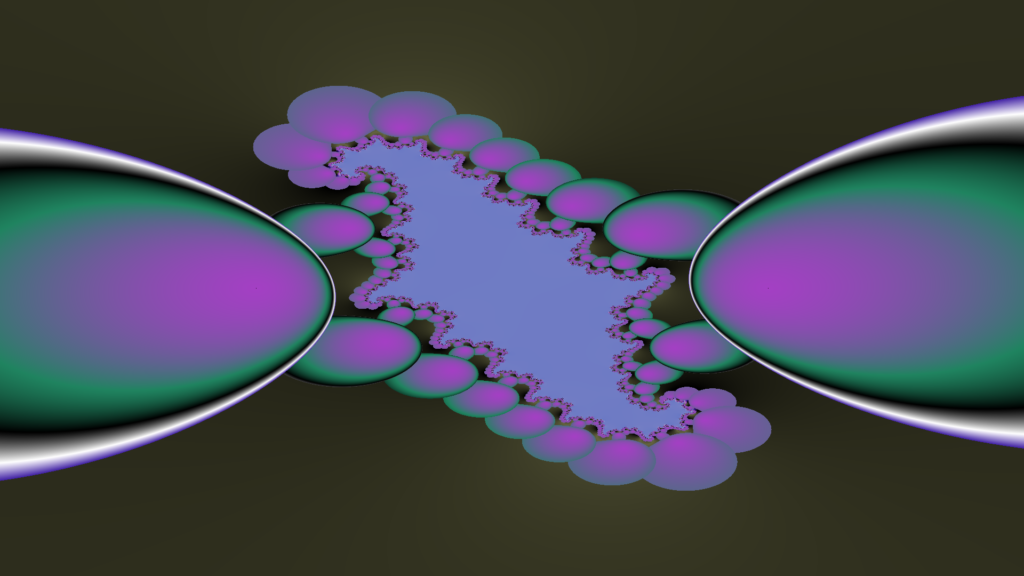
d=-0.075189+1.8490056i

d=-0.34655476-0.6482633i

d=0.6521721+0.664937i